Modelo general de las funciones
polinomiales.
En
matemáticas, una función polinómica
es una función asociada a un polinomio.
Formalmente, es una función:
“n “es un número natural y se
llama el grado del polinomio, Los números an, an−1,···, a1, a0
son números reales y son los coeficientes del polinomio. Se pide que an ≠ 0.
Dicho
de otra forma: es un polinomio definido para todo número real x; es decir, una suma finita
de potencias de x, multiplicados
por coeficientes reales, de la forma:
Forma y representación gráfica de
funciones polinomiales de grado: cero, uno, dos, tres y cuatro
El
grado de un polinomio está dado por el mayor exponente de la variable en el
polinomio, independientemente del orden en el que estén los términos, como se muestra en las siguientes funciones:
1.
f(x) = 7.
Es de grado cero, se le conoce como función
constante.
2.
f(x) = 4x − 1. Es de grado uno, también
conocida como función lineal.
3.
f(x) = x2
+ 5x + 6. Es de grado dos, se le conoce como función
cuadrática.
4.
f(x)= 4x2
+ 5x3 + 1. Es de grado tres y se le conoce como función cúbica
5.
f(x)= 4x4
+ 3x3 + 2x2 + 1. Es de grado cuatro y se
le conoce como función cuartica.
FUNCIONES
POLINIMIALES GARDO CERO (características y parámetros)
La función constante. La función de grado cero es la que se
conoce como función constante, ésta es un caso particular de la función
Polinomial y se inició con ella en el primer bloque; su forma es:
F (x
) = a, donde “a” es
una constante
Su gráfica es una recta paralela al eje X y corta al eje Y
en el punto (0, a).
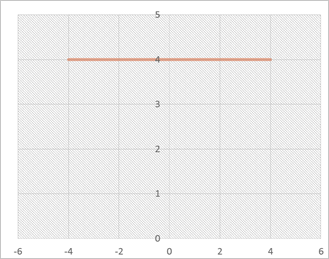
Graficar la función f(x) = 5,
determinar su dominio y rango.
La función también se puede expresar como y = 5, por lo tanto su gráfica
es una recta horizontal a la altura de 5, como se muestra en la siguiente
figura.
Dominio (−∞, ∞), y
su contradominio{5}
Se debe recordar que el dominio de un polinomio siempre
será 𝑅 = (−∞, ∞)
FUNCIONES
POLINIMIALES GARDO UNO (características, parámetros y aplicaciones)
La ecuación lineal en su forma
pendiente-ordenada en el origen es:
y = mx + b
Donde m es la pendiente de la recta y b es la ordenada del
origen. Vista como una función se representa de la siguiente manera:
F(x) = mx +
b
Dónde:
b Es
la constante que indica el lugar donde la recta cruza el eje y, además se le denomina término independiente.
m.
Es la pendiente de la recta, la cual está relacionada con su inclinación, es el coeficiente de la variable.
x. Es la variable independiente.
En la siguiente figura se muestra la función de los
parámetros antes mencionados.
F(x) = 2x+3
Aplicaciones
Funciones de proporcionalidad
directa
Las funciones
polinómicas de primer grado con término independiente cero, representan la
relación entre dos variables directamente proporcionales. Por ejemplo.
Supongamos que
el kilogramo de naranja tiene un valor
$8 pesos. Para saber el precio de X
cantidad de kilos. Nuestra función quedaría expresada de la siguiente manera.
F(x) = 8x
Las funciones polinómicas de
primer grado con término independiente, representan la relación entre dos
variables directamente proporcionales y el aumento o disminución de la variable
independiente. Por ejemplo.
El costo por
llamada local es de $5 pero minuto, si es una llamada de larga distancia se
cobrara roming adicional que es de $3 por llamada. ¿Cuál será el costo de una
llamada de X minutos?
F(x) = 5x+3
FUNCIONES
POLINIMIALES GARDO DOS (características, parámetros y aplicaciones)
Las funciones cuadráticas se
caracterizan por su grado 2, éstas se expresan en su forma general como f(x) = ax2 + bx + c, con la condición de que su
coeficiente principal es diferente de cero (a ≠ 0) se compone de la
siguiente manera:
ax2= Término cuadrático.
bx=. Término
lineal.
c.= Termino
independiente.
La clasificación de las
ecuaciones cuadráticas depende de los términos que aparezcan en ellas. Se les
llama completas cuando poseen todos los términos, e incompletas cuando carecen
de alguno. Si no tiene el término lineal se denominan puras, y si no aparece el
término independiente se conocen como mixtas.
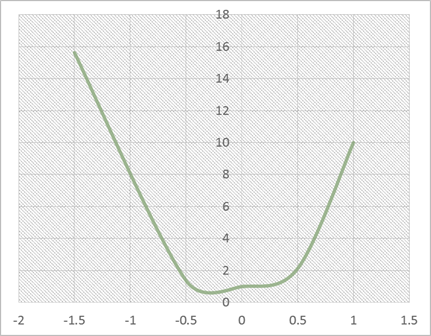
Las gráficas de las funciones
cuadráticas describen parábolas, como se muestra en la siguiente figura.
Dependiendo del tipo de parábola
(con ramas hacia abajo o ramas hacia arriba), el vértice es el punto mínimo o
punto máximo, como se muestra en la siguientes
figuras.
APLICACIONES
Mediante las funciones
polinómicas de segundo grado se pueden estudiar algunas situaciones, presentes
en el mundo físico y la vida real.
Además el vértice de la parábola,
es el máximo o mínimo relativo y a la vez absoluto de la función cuadrática
correspondiente; mínimo si es convexa (hacia arriba) o máximo si es cóncava
hacia abajo. Entonces para calcular los extremos relativos de estas funciones
basta calcular las coordenadas del vértice, como puedes observar en los
ejemplos siguientes.
1) Movimiento uniformemente acelerado
2) Rectángulo de área máxima
3) Punto de no retorno
FUNCIONES
POLINIMIALES GARDO TRES (características y parámetros)
Son las de la forma y = ax3 + bx2 + cx + d
, siendo a , b , c y d números reales y a≠0.
Todas estas funciones tienen
dominio y contradomido (-∞,∞) y
son continuas. Respecto de los puntos de corte con los ejes podemos decir que
la gráfica puede cortar al eje de abscisas(eje Y) en 1, 2 ó 3 puntos y al eje
de ordenadas (eje X) siempre en el punto (0,d)
Las gráficas de estas funciones
cúbicas son de cuatro tipos exclusivamente, que distinguiremos por los extremos
y los puntos de inflexión :
- Sin extremos, el punto de
inflexión separa la región cóncava de la convexa o la convexa de la cóncava.
- Con dos extremos, un máximo y
un mínimo, el punto de inflexión separa la región convexa de la cóncava o un
mínimo y un máximo, separando el punto de inflexión la región cóncava de la
convexa.
CASO 1: y = ax3. Estamos
en el caso de que b, c y d son nulos. Son funciones que tienen un único punto
de corte con los ejes que es el (0,0), no tienen extremos y son crecientes
si a > 0 y decrecientes si a < 0. Al
variar "a" podemos observar que si toma valores cada vez mayores la
función se acerca al eje OY y si los valores de "a" son más pequeños
se ensancha.
CASO 2: y =
ax3 + d Estamos en el caso de que b y c sean nulos. Estas
funciones tienen dos puntos de corte con los ejes, uno con el 0X y otro con el 0Y,
no tienen extremos y son crecientes si a > 0 y decrecientes si a < 0.Su
gráfica se obtiene trasladando la de la
función y = ax3 , d
unidades en la dirección del eje 0Y. Al variar d, se puede ver que si d > 0
la traslación es hacia arriba y si d < 0 la traslación es hacia abajo
CASO 3: y = ax3 + bx2: En este nuevo
caso c y d son nulos. Son funciones que tienen como puntos de corte (0,0) y
(-b/a,0) , los extremos están en los puntos de abscisas x = 0 y x = -2b/3a
(todas las funciones de este caso tienen un máximo y un mínimo) y el punto de
inflexión está en x=-b/3a.
CASO 4: y = ax3 + cx. En este último
caso particular b y d son nulos. Dependiendo de los valores de a y c sólo hay
dos familias de gráficas:
CASO 5: CASO
GENERAL y = ax3 +bx2 + cx + d
FUNCIONES
POLINIMIALES GARDO CUATRO (características y parámetros)
Es la función de fórmula: y =
ax4+ bx3+ cx2+ dx+ e; donde a (distinto de 0), b, c, d y e son números reales.
En la función cuártica el dominio es el conjunto de números
reales, pero el rango sólo es una parte de ellos.
Los parámetros tienen el mismo
efecto que en la función de grado dos (cuadrática); en el caso que el parámetro
“a” sea positivo la función tiende infinitamente hacia arriba, si el parámetro
“a” es negativo, la función tiende infinitamente hacia abajo.
Cuando se conoce la función estándar de una
función cuártica, se puede conocer el punto máximo o mínimo, esto dependerá del
signo del parámetro “a”.
ACTIVIDADES:
1.- Completar la siguiente tabla, donde para cada función
polinomial se identifica su término independiente y grado
2. En cada caso haz una tabla de valores y gráfica correspondiente
(Realiza todos los trazos en el mismo plano).
a) f(x)=3
b) f(x)=-2x+3
c) f(x)=x2-x+2
d) f(x)= x3+x2+x-4
e) f(x)=x4+x3-x2+x+5
3.- Resuelve cada uno de los siguientes ejercicios
1. Escribe la ecuación de la función que representa el
peso de un caballo si nace con 30 kg y aumenta a razón de 1 kg cada 2 días.
2. Escribe la ecuación de la función que representa el
precio al finalizar la conexión en un ciber, si el establecimiento de la
conexión cuesta 0,10 € y cada minuto vale 0,03 €.
3. Escribe la ecuación de la función que representa el nº
de la página del libro que estoy leyendo, sabiendo que todos los días avanzo el
mismo nº de páginas, el día 10 iba por la 290, y el día 17 por la 465.
4. Escribe la ecuación de la función que representa la
cantidad total en € (IVA incluido) a pagar en una factura, en función del
precio sin IVA, sabiendo que el porcentaje de aumento aplicado es del 16%.
5. Calcula el valor de b para que la gráfica de la
función f(x)=2x2+bx-4, pase por el punto (-3, 2).
6.- Escribe la ecuación de la parábola que tiene
coeficiente a=1, corta al eje de ordenadas en (0, -3) y su vértice es el punto
(-2, -7).
NOTA: LAS ACTIVIDADES LAS RECIBIRÉ EL DÍA MARTES 19 DE 1-1:30 O EL MIÉRCOLES 20 DE 11-11:30 EN COORDINACIÓN DE COBACH (POR EL DEPORTIVO)